Ybus is the admittance matrix. It is highly sparse. Its inverse is a full
matrix Zbus. For short circuit application, only the neighborhood Z(i,j) of a faulted
bus is needed to calculate fault current contributions. So instead of solving the
entire Zbus, only a few elements will be calculated. Those few elements are said to
be "sparse Zbus". These are calculated from the factors (L,U) of the sparse Ybus. For the mathematicians, we can simply say, "Given the factored of a sparse matrix,
we can solve any element/s of its inverse without solving the entire inverse."
The following derivation is easy to understand compared to Ref. [7].
By definition,
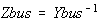 --- Eq.(1) and
--- Eq.(1) and
Ybus * Zbus = I --- Eq. (2)
where I = identity matrix. Let L*U = Ybus so,
L*U*Z = I
--- Eq. (3)
In order to solve Z, given the LU of Ybus, let
U*Z = X --- Eq. (4)
Then L*X = I --- Eq. (5)
where X is the unknown matrix. X can be solved by performing matrix multiplication. After X is
known, solve for Z in the Eq. (4) also by matrix multiplication. The structure of matrices L and U for
a 4x4 size (you can generalize and use size n with three
dots,like 1,2, ... , n ) are,
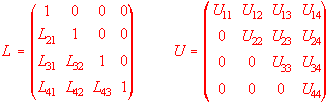 Eq. (6)
Eq. (6)
We can derive the equations involved in sparse Zbus matrix using the
expanded example for a 4x4 matrix size. From Eq. (5) L * X = I
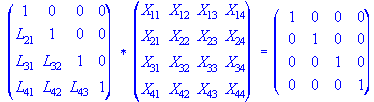 Eq. (7)
Eq. (7)
Note here the difference between the famous LDU nomenclature
of Ref. [17]. By matrix multiplication, solving each row in [I], we have:
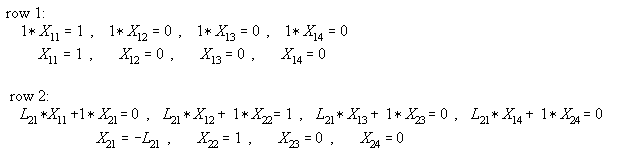
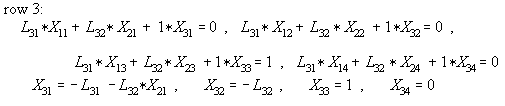
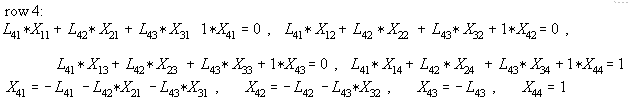
In matrix form, [X] is:
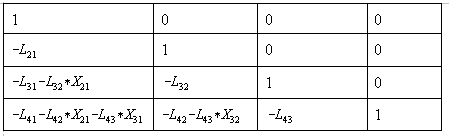 Eq. (8)
Eq. (8)
Where the lower off-diagonals will not play a role in the next
process. The L matrix seems not to affect Eq (3). Recall the
property that when a matrix is symmetrical, the factors [L], [U]
can be stored only as [U], i.e. as half-storage and [L] can be
calculated simply by dividing each element U(i,j) by U(i,i)
which now is L(j,i).
Solving Eq. (4) U*Z = X by expanded example,
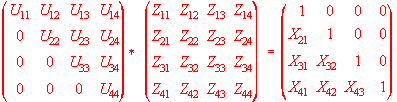 Eq. (9)
Eq. (9)
Solving for by matrix multiplicattion, and we will solve only the upper
triangle, knowing that Zbus is symmetric;
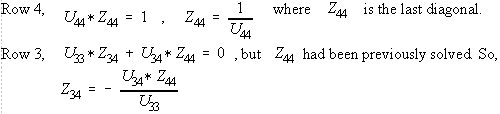
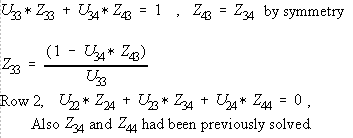
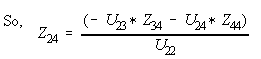
Note that 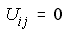 if no connection exists in Ybus, however
if no connection exists in Ybus, however
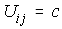 for a fill-in in LU after factoring Ybus, which is previously zero as no impedance is connected between i and j. Fill-ins are needed to solve the elements of Zbus. They become part of the LU.
for a fill-in in LU after factoring Ybus, which is previously zero as no impedance is connected between i and j. Fill-ins are needed to solve the elements of Zbus. They become part of the LU.
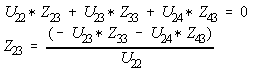
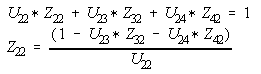
In general
form,

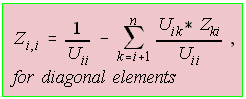 --- Eq. (10)
--- Eq. (10)
8.2 Example Calculation
Given the factored form of Ybus matrix and only U is stored,
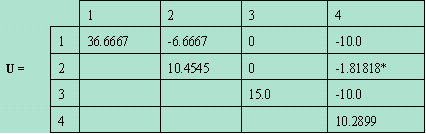
* Y(2,4) is a fill-in
Let the matrix L*U be stored on Y itself.
Z(4,4) = 1/Y(4,4) = 1/10.2899 = 0.097183
Z(3,4) = - Y(3,4)*Z(4,4)/Y(3,3)
= 10 * 0.097183/15 = 0.0647887
Z(3,3) = 1/Y(3,3) - Y(3,4)*Z(4,4)/Y(3,3)
= 1/15 + 10 * 0.064788/15 = 0.06667 + 0.043192
= 0.109859
Z(2,4) = -Y(2,3)*Z(3,4)/Y(2,2) - Y(2,4)*Z(4,4)/Y(2,2)
= 1.81818 * 0.097183/10.4545
= 0.0169014
Where Z(2,4) is a fill-in, it is needed in solving other elements.
Y(2,3)=0. If Y(i,j)=0, it means there is no impedance connecting i and j.
If it becomes nonzero after mutual coupling compensation or after the LU
factorization, its Z(i,j) should be solved.
Z(2,3) is not needed since for NBACK=1 , it will not participate in
flow contribution. We will understand the meaning of NBACK later.
Z(2,2) = 1/Y(2,2) - Y(2,4)*Z(4,2)/Y(2,2)
= 1/10.4545 + 1.81818 * 0.0169014/10.4545
= 0.095652 + 0.00293938
= 0.0985916 where Z(4,2) = Z(2,4)
Z(1,4) = -Y(1,2)*Z(2,4)/Y(1,1) - Y(1,3)*Z(3,4)/Y(1,1) - Y(1,4)*Z(4,4)/Y(1,1)
= 6.6667 * 0.0169014/36.6667 + 10.0* 0.097183/36.6667
= 0.003072994 + 0.026504
= 0.0295775 where Y(1,3)=0
Z(1,3) same reason as Z(2,3)
Z(1,2) = -Y(1,2)*Z(2,2)/Y(1,1) - Y(1,4)*Z(4,2)/Y(1,1)
= 6.6667 * 0.0985916/36.6667 + 10.0*0.0169014/36.6667
= 0.0179258 + 0.00460946
= 0.0225352
Z(1,1) = 1/Y(1,1) - Y(1,2)*Z(2,1)/Y(1,1) - Y(1,3)*Z(3,1)/Y(1,1)
- Y(1,4)*Z(4,1)/Y(1,1)
= 1 / 36.6667 + 6.6667*0.0225352/36.6667 + 10.0*0.0295775/36.6667
= 0.02727 + 0.0040973 + 0.0080665
= 0.0394366
|

8.3 Code Fragments on Direct Zbus Formation
Code=1: Programming in full matrix.
1: Z[nb][nb]=1/U[nb][nb];
2: for (i=nb-1;i>=1;i--)
3: { for (j=nb;j>=i;j--) //j>=i means upper triangle only, lastly j=i
4: { Z[i][j]=0.0; // initialize accumulator
5: if (U[i][j]) // solves only non-zero Ybus
6: for (k=i+1;k<= nb;k++)
7: if (U[i][k]) //exclude zero operation
8: {Zkj=GetZij(Z,k,j); // only upper triangle
9: Z[i][j]-=U[i][k]*Zkj/U[i][i];
10: }
11: } /*for j*/
12: Z[i][i]+=1/U[i][i];
13: } /*for i*/
Code=2: Programming in full matrix,to simulate Sparse Code.
1: Z[nb][nb]=1/U[nb][nb];
2: for (i=nb-1;i>=1;i--)
3: { for (j=i+1;j<= nb;j++) //note the start of j
4: { Z[i][j]=0.0;
5: if (U[i][j]) //solve only sparse Z
6: {for (k=i+1;k<= nb;k++)
7: if (U[i][k]) //exclude zero operation
8: {Zkj=GetZij(Z,k,j);
9: Z[i][j]+=Uik*Zkj; //the summation part
10: }
11: Z[i][j]=-Z[i][j]/U[i][i]; //only one division
12: Z[i][i]+=U[i][j]*Z[i][j]; // Zij is correct already
13: } /*if U[i][j]*/
14: } /*for j*/
15: Z[i][i]=(1-Z[i][i])/U[i][i]; //Zii is correct already
16: } /*for i*/
Code=3: Programming in sparse matrix, without Ordering Y=U
1: void Zbus()
2: {int k,i,j,ij,ik,kj,J,K,EndBus[20],Adr[20],counter;
3: Zd[nb]=1/Yd[nb]; /*last Zbus diagonal, will not work if Yd[nb]=0.0
4: for (i=nb-1;i>=1;i--)
5: {counter=Get_RHSnodes(i,EndBus,Adr); //counter=rhs nodes count
6: if (counter)
7: {for (j=1;j<= counter;j++)
8: {J=EndBus[j];ij=Adr[j];
9: for (k=1;k<= counter;k++)
10: {K=EndBus[k];ik=Adr[k];
11: if (J==K) {Z[ij]+=Y[ik]*Zd[J];} //needs diagonal Zjj, when k=j
12: else {kj=BrnSrOnly(K,J);
13: Z[ij]+=Y[ik]*Z[kj];} //the summation part
14: } /*for k*/
15: Z[ij]=-Z[ij]/Yd[i]; //Zij is correct already
16: Zd[i]+=Y[ij]*Z[ij];
17: } /*for j*/
18: } /*if counter*/
19: Zd[i]=(1-Zd[i])/Yd[i]; //Zii is correct already
20: } /*for i*/
21: }
Code=4: Programming in sparse matrix, with Ordering Y=U
1: void Zbus()
2: {int k,i,ii,j,ij,ik,kj,J,K,EndBus[20],Adr[20],counter;
3: ii=NewOrder[nb];Zd[ii]=1/Yd[ii];
4: for (ii=nb-1;ii>=1;ii--)
5: {i=NewOrder[ii];counter=Get_RHSnodes(i,EndBus,Adr); //counter=rhs nodes count
6: if (counter)
7: for (j=1;j<= counter;j++)
8: {J=EndBus[j];ij=Adr[j];
9: for (k=1;k<= counter;k++)
10: {K=EndBus[k];ik=Adr[k];
11: if (J==K){Z[ij]+=Y[ik]*Zd[BusPtr[J]];}//needs diagonal Zjj,when k=j
12: else {kj=BrnSrOnly(K,J);
13: Z[ij]+=Y[ik]*Z[kj];} //the summation part
14: } /*for k*/
15: Z[ij]=-Z[ij]/Yd[i]; //Zij is correct already
16: Zd[i]+=Y[ij]*Z[ij];
17: } /*for j*/
18: Zd[i]=(1-Zd[i])/Yd[i]; //Zii is correct already
19: } /*for i*/
20: }
|
Analysis of the code.
In Code=1, j starts from nb and moves towards i. The Zij solved will thus include Zii. It can not start from j=i to nb because it must first solve Zij (j>i) elements. These elements are needed in solving for Zii. When j=i, we are`solving the diagonal Zii,Z[i][i]-=Y[i][k]*Zki/Y[i][i], where Zki is already correct, thus the equation still follows that for Zii. After the j loop, Zii lacks 1/Uii. The off-diagonal
terms Z[i][j] are already correct after the k loop. The sparsity check on Line_5 for a zero Y[i][j] is not a good check because there are cases where due to LU factorization a previously non-zero becomes zero. We still have to solve for Zij even if Yij becomes zero because skipping Y[i][k]*Z[k][j] will result to an error in Z[i][i]. For sparse matrix, this would not pose a problem, because only non-zero Y's are stored and accessed.
In Code=2 j starts from i+1. This will mimic the sparse code for Code=3. The division takes place once the summation is finished. Computationally, it is better to divide once. In the k-loop, summation in plus is used instead of minus. After the k-loop is finished, negate first then divide by Yii. Zij is computed already in correct sign. That finished Zij can now be used in Zii. The summation in Zii is also plus. After the j-loop is through Zii=(1-Zii)/Yii.
Codes=3 and 4 are essentially the same. In code=4, an order is used. Both calls to "Get_RHSnodes(i,EndBus,Adr)" has i=compact bus number. Accessing for YPd in code=4 uses YPd[BusPtr[I]] instead of YPd[I] only. Searching for "kj=BrnSrOnly(K,J)" does not insert branch K->J. When the process being performed is LU Factorization, a branch is inserted if it is absent. The algorithm has an error if branch K->J is not in lifo. The error may lie in the LU subroutine.
8.4 Simulating Sparse Zbus from factored Sparse Ybus

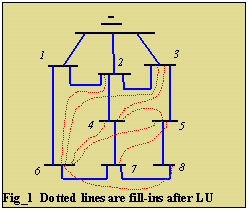
Shown on the table above is the input data for the circuit on figure_1. The dotted
lines are the off-diagonal elements representing the fill-ins after the LU factorization.
Scheme Ordering was not applied.
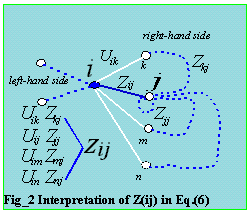
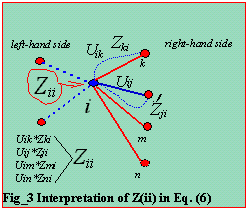
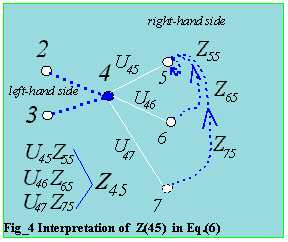
Figure_2 is a graphical representation of equation (6) to solve for the off
diagonal Zbus elements, while Figure_3 is for the diagonal elements.
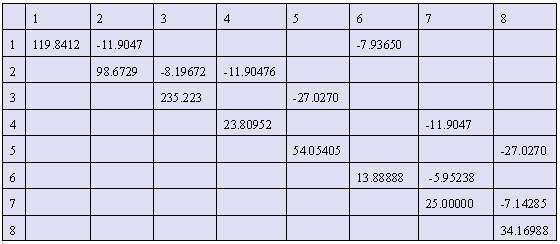
The table above is the complete zero sequence Ybus matrix. Only the diagonal and
the upper triangle is stored. In this example, there
is no mutual coupling. We are to solve for the sparse Zbus from
factored Ybus. The blank or zero part indicates that there is no impedance
connection between those i-j nodes.
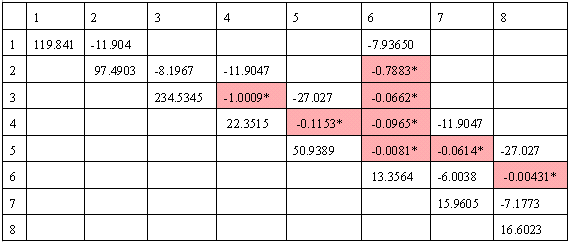
The table above is the Factored Zero Sequence Ybus. The 8 elements in different
color are the fill-ins. Sparse Zbus to be solved must be in a one-to-one correspondence as the factored Ybus, even though some of them are now zero after factorization, provided they were non-zero before factorization. Why? Because they define network topology. Rhs
(right hand side) Zbus elements corresponding to its topology is needed in solving for Zbus diagonal element. Remember that Zbus is full and nonzero. With lifo, we do not have a problem since each element in the factored Ybus is accessed by the linked-list.
Using the program, we can output the required U's and Z's and thus visualize Eq. (6) better. The contents inside the textarea are not the complete equation, only the
required multiplication pairs in the "summation".
For row=4, the sparse Zbus required to be solved are Z(4,7), Z(4,6), Z(4,5). The
diagonal element is Z(4,4). Only the right hand side need be solved. Note that Z(4,8)
is not required in the sparse Zbus. Try scrolling the textarea and look for Z(4,8).
In solving for Z(i,j) of a row, each can be solved in any order. That is, Z(4,5) can
be solved ahead of Z(4,7). But all these [Z(4,7), Z(4,6), Z(4,5)] are needed for Z(4,4).
The 3 figures below are graphical representation for the off-diagonal Z(i,j)s.
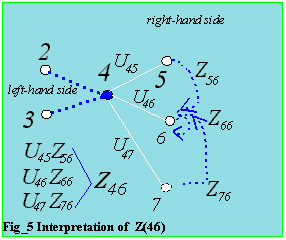
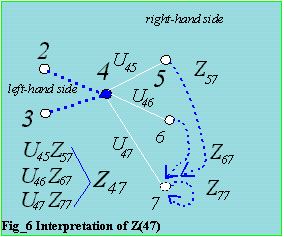
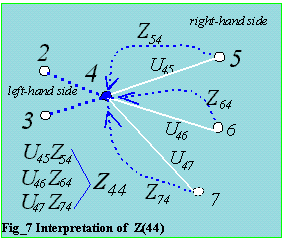
The figure below is for the diagonal, the off-diagonals are needed.
The table below is the sparse Zbus as computed by the program. The term "sparse Zbus"
is not really accurate because Zbus is not sparse. Zbus is a full matrix. However, the sparse Zbus we are referring to has the exact sparseness as the factored Ybus.
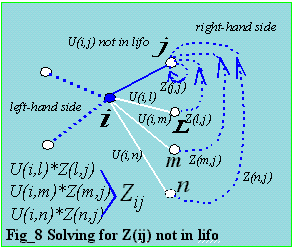
Solving for Zij not in the Link List
The textarea below solves all the Zij's. Those not in the lifo have an arrow inluded.
We would like to determine what are the summation
pairs required for a particular Zij. Figure_8 is the graphical representation. Nodes
L,M,N are the in the lifo, while i,j is not. This figure is similar to
figures_4,5,6 when determining the summation pairs needed with respect to Uij elements.
Legend: "==>" are Zij not on the lifo
The table below is a full Zbus.
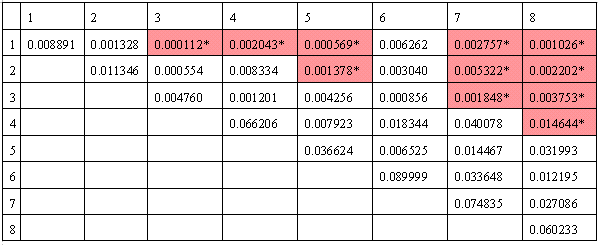
where Z(i,j) with asterisk (*) are zeroes in Y(i,j) after LU.
Example Z(2,5) requires U(2,3)*Z(3,5), U(2,4)*Z(4,5), and U(2,6)*Z(6,5). The elements U(2,3), U(2,4), and U(2,6) are still the non-zero U(i,k), and Z(3,5), Z(4,5), and Z(6,5)=Z(5,6) are also present in Sparse Zbus.
Another example Z(1,5) requires U(1,2)*Z(2,5), U(1,6)*Z(6,5) . Z(5,6) is present in Sparse Zbus, but Z(2,5) is not. The elements not in lifo are included when solving for Zij, for NBACK greater than 1. The procedure would be to sort all required Zij according to node ordering, before solving for their values.
8.5 Output for NBACK greater than 1
The lifo for Ybus/Zbus and line impedance both for positive and zero sequence is just one. To output for NBACK>1, Zij not in lifo will be solved and placed in a separate vector.
From Fig_8,i,j is not in lifo. To solve for Zij, we will need only 3 pairs, U(i,l)*Z(l,j), U(i,m)*Z(m,j), and U(i,n)*Z(n,j). The elements U(i,l), U(i,m), and U(i,m) are the factored Ybus and accessible in lifo. The other terms Z(l,j), Z(m,j), and Z(n,j) must be searched in lifo. If not present, say Z(m,j), this too must be solved, recursively. This recursion will not be infinite because we are solving only the rhs terms. For a fault on bus=1, flow on line 6-7 requires Z(1,6) and Z(1,7). Z(1,6) is present in lifo but Z(1,7) is not. To solve,
Z(1,7)=U(1,2)*Z(2,7)+U(1,6)*Z(6,7). Z(6,7) is present but Z(2,7) is not. So solve
Z(2,7)=U(2,3)*Z(3,7)+U(2,4)*Z(4,7)+U(2,6)*Z(6,7). Again Z(4,7) and Z(6,7) are present but Z(3,7) is not. Again solve
Z(3,7)=U(3,4)*Z(4,7)+U(3,5)*Z(5,7)+U(3,6)*Z(6,7) and this time all Z(4,7), Z(5,7), and Z(6,7) are all present. Therefore to solve for Z(1,7), it is necessary first to solve for Z(2,7) and Z(3,7).
If it is required to solve the entire branch contributions then the entire column corresponding to the faulted bus must be solved. Will you be required to solve the entire Zbus? No. Only additional Zij elements needed are those corresponding to a branch defined in the topology. If m,n,l,k are the only nodes connected to faulted node i, then additional elements are required for Zim,Zin,Zil and Zik and all the rest will need only those already solved in the column.
8.6 Description of Computer Programs for this Chapter
There are 3 programs in this Chapter. Described are its features and limitations.
It is good to have this "textarea" in HTML format. It is like having a bird's eye
view of the earth. If the bird wants worm, he just dive down. This "textarea"
is analogous, just dive down by scrolling. Each program is created in increasing
complexity.
1. SPARZE_Z.C
a. Contiguous numbering
b. Not complex number
c. Mutual coupling, LU factorization, Fault Calculation included
d. Full matrix but solves Upper triangle only for Ybus and Zbus
2. CPLEX_Z.C
a. Contiguous numbering
b. Complex numbers, demonstrates friend operators and classes
c. Mutual coupling, LU factorization included
d. Full matrix but solves Upper triangle only for Ybus and Zbus.
3. LIFO_YZ.C
a. Contiguous numbering, no ordering yet
b. Complex numbers, demonstrates friend operators and classes
c. Mutual coupling, LU factorization included
d. Sparsity Techniques used and solves Upper triangle only for Ybus and Zbus.
e. Coupling on Parallel lines allowed
f. Sorted branches, parallel lines have negative branches
g. Fill-ins have negative circuit numbers
h. Can not process infinity impedance and no test for islands
8.7 Formation of a Column of Zbus from Factored Ybus.
We will slightly alter the topic in 8.1 and instead of solving a sparse Zbus, we solve a complete column of the Zbus. Given a complete column, we can display fault contribution of the entire network, i.e., NBACK=all. If we wanted NBACK=1 only, then use the topics 8.1 to 8.6. Solving a chosen column does not require to solve any other Zij from other columns. This topic may be used in other branch of engineering that requires to solve one or several columns of an inversed matrix, without solving the entire inverse. This chapter must be read independent of 8.1 as sometimes it is confusing if you compare the two. We do not have to worry if the gifs are redisplayed here as you are reading a computer file, not a printed page.
By definition,
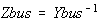 --- Eq.(1) and
--- Eq.(1) and
Ybus * Zbus = I --- Eq. (2)
where I = identity matrix. Let L*U = Ybus so,
L*U*Z = I
--- Eq. (3)
In order to solve Z, given the LU of Ybus, let
U*Z = X --- Eq. (4)
Then L*X = I --- Eq. (5)
where X is the unknown matrix. X can be solved by performing matrix multiplication. After X is
known, solve for Z in the Eq. (4) also by matrix multiplication. The structure of matrices L and U for
a 4x4 size (you can generalize and use size n with three
dots,like 1,2, ... , n ) are,
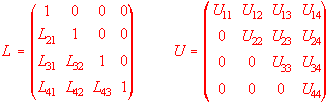 Eq. 6
Eq. 6
We can derive the equations involved in sparse Zbus matrix using the
expanded example for a 4x4 matrix size. From Eq. (5) L * X = I
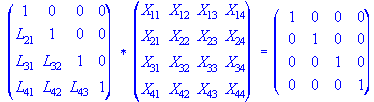 Eq. 7
Eq. 7
Note here the difference between the famous LDU nomenclature
of Ref. [17]. By matrix multiplication, solving each row in [I], we have:
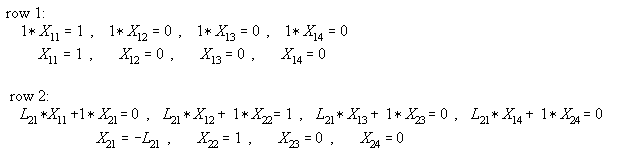
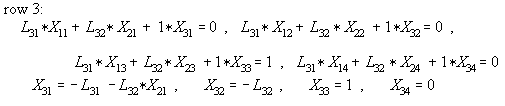
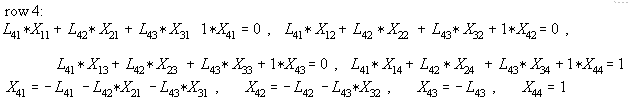
In matrix form, [X] is:
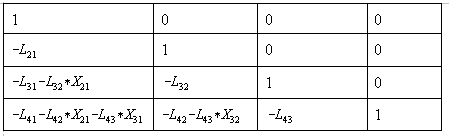 Eq. 8
Eq. 8
Recall the property that when a matrix is symmetrical, the factors [L], [U] can be stored only as [U], i.e. as half-storage and [L] can be calculated simply by dividing each element U(i,j) by U(i,i) which now is L(j,i). Up to this point, we can already derive the general equation for forward course, but will delay it. The purpose is to present the subject matter in an orderly manner and understand the procedure more easily. We have not discuss yet how to solve a chosen column. The equation above represents all the columns. Compare the derivation here with "Power System Analysis" by Grainger and Stevenson.
Now, we substitute X in Eq. (4) U*Z = X and assuming X contains the computed values already. Showing the equation in matrix (size 4x4) will be,
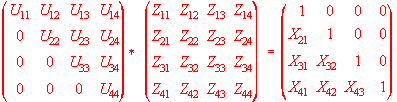 Eq. 9
Eq. 9
Using Eq. 9, any column of Zbus can be solved. Similarity in the derivation in Chapter 8 ends here. The next gifs below shows what the matrix equation would be when column 1,2,3 and 4 are solved.
 Eq. 10
Eq. 10
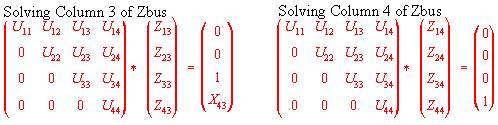
We will not solve all these columns. Just try column 2. What is special with column 2? There is nothing special, we can derive the general equation for backward course with any column because the right hand side term is stored on a vector and we do not care about its value. By observation, location for ibus (the chosen column) is still 1 and zeroes from ibus-1 to 1. Unlike the forward course where this is relevant in the programming aspect, in backward course this is not the case. The equation is valid from node 1 to nb (the last node). This backward course is similar to the process in Loadflow. The difference is that, in here the quatities are complex numbers. Why can we not do complex numbers in loadflow? We start from the bottom, that is why it is called backward course.
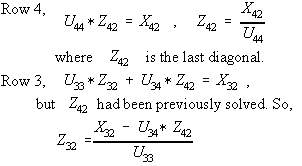
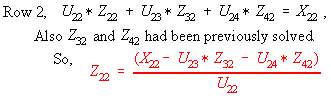 Eq. 11
Eq. 11
We can now write a general equation by observing the subscripts. The ibus is the chosen column and k represents all node connections to row i (or node i). The summation says that k starts from (i+1), which means these are the right hand side terms of the matrix. Left hand side terms do not participate. So in sparse matrix applications, only the rhs members of the lifo are needed. We solve from i=N or nb (the last bus) up to bus=1 and -1 means decrementing.
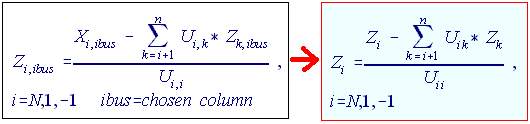 Eq. 12
Eq. 12
This represents the complete column. We may remove the subscript ibus in the equation because we are not storing the chosen column of Zbus in a
square matrix, rather in a vector. Also, there is no need to store X and Z in separate vectors. Try to visit the Forward/Backward course topic, X and Z is stored in one vector. We can now rewrite the general equation as shown by the red arrow.
 | Forward course can be better understood by expanding the 4x4 size matrix to 8x8. In here we chose ibus=5. By performing row multiplications, X[1], X[2], X[3], X[4] yield zeroes. So we may conclude that {X[i]=0 for i=1 to ibus-1 and X[ibus]=1.0}. If we are using complex numbers, it should be 1.0 +j0.0.
X[5]=1 - - - Eq. 13
X[6]= - L[6][5]*X[5]
X[7]= - L[7][5]*X[5] - L[7][6]*X[6]
X[8]= - L[8][5]*X[5] - L[8][6]*X[6] - L[8][7]*X[7]
|
In this example X[] prior to the chosen column is zero and it would be a waste if we include them in the computation. Using lifo and accessing the elements in the row, or the left-hand side of the diagonal is not good as we have to test for connections from 1 to ibus-1 and exclude the value of X[]. Instead we use downward connections which is equivalent to RHS connections. For each loop, X[i] will be completed. By examining Eq. 13, there is no need to solve for X[ibus]. But X[ibus] is a multiplier to all connections to ibus. Also, there is no product of X[8]. So, the outer loop should be {for (i=ibus to nb-1}. The inner loop represents all connections to node i except the diagonal. The inner loop must be {for k=i+1 to nb}. Who gets the update? X[k], where k are the node connections to i. For sparse matrix, instead of using (k=i+1 to nb}, just use all RHS node connections. All these RHS nodes get the update. We can not write a general equation to represent the forward course, but instead we derive what the inner and outer loops should be. The code snippet for the full matrix and sparse matrix shows the underlying principle;
FOR FULL MATRIX
for (i=1;i<=nb;i++) //reset the column of Zbus
Z[i]=0.0;
Z[ibus]=1.0; //set to 1 the chosen column
//Forward Course
for (i=ibus;i<nb;i++) //Update all nodes connected to ibus to nb-1
for (k=i+1;k<=nb; k++)
Z[k]-=Z[i]*U[i][k]/U[i][i];
//the last Zbus //Backward Course
Z[nb]/=U[nb][nb];
for (i=nb-1;i>=1;i--)
for (k=i+1;k<=nb;k++)
Z[i]-=U[i][k]*Z[k];
Z[i]/=U[i][i];
SNIPPET FOR SPARSE MATRIX
for (i=1;i<=nb;i++)
Z[i]=0.0;
Z[ibus]=1.0;
//Forward Course
for (i=ibus; i<nb;i++)
{counter=get_RHSnodes(i,neighbor,adres);
//counter is the number of RHS nodes, excludes parallel branches
//impedance address of branch connections is stored in adres[]
//node number for that address is stored in neighbor[]
for (k=1; k<=counter; k++)
{busk=BusPtr[neighbor[k]];
Z[busk]- = U[adres[k]]*Z[i]/Ud[i];
//only a few busk will get an update
}
}
//Backward Course
Z[nb]/=Ud[nb];
for (i=nb-1; i>=1,- -i)
{counter= get_RHSnodes(i);
for (k=1;k<=counter;k++)
{busk=BusPtr[neighbor[k]];
Z[i] - = U[adres[k]]*Z[busk];
}
Z[i]/=Ud[i];
}
|
8.8 Description of Computer Program to Solve a Column, Full Matrix
COLUMN.CPP
a. Contiguous numbering
b. Not complex number
c. Mutual coupling, LU factorization
d. Full matrix but solves Upper triangle only for Ybus
e. Solves a column of Zbus, any column.
Code Explanation:
This code contains subroutines similar to those in chapter 5 and 8, like the creation of Ybus, LU factorization and reading of input data. The only new part here is the subroutine Zbus. Only one vector stores Z[] and X[]. In line_301, the loop is from 1 to nb (the last bus). We included index from ibus+1 to nb because the forward course requires to perform some summation on them.

HOME
CHAPTER ONE: INTRODUCTION
CHAPTER TWO: PROGRAMMING TOPICS
CHAPTER THREE: MATRIX INVERSION ROUTINE
CHAPTER FOUR: STEP-BY-STEP ALGORITHMS
CHAPTER FOUR: Part 2
CHAPTER FIVE: DIRECT METHODS IN Ybus FORMATION
CHAPTER SIX: SPARSITY
CHAPTER SEVEN: MATRIX FACTORIZATION AND OPTIMAL ORDERING
CHAPTER EIGHT: SPARSE Zbus FROM FACTORED SPARSE Ybus
CHAPTER NINE: FAULT CALCULATIONS
REFERENCES
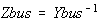 --- Eq.(1) and
--- Eq.(1) and
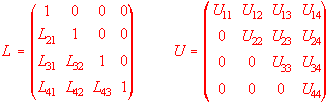 Eq. (6)
Eq. (6)
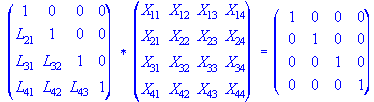 Eq. (7)
Eq. (7)
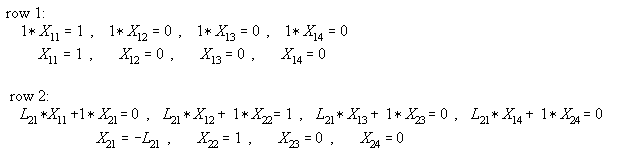
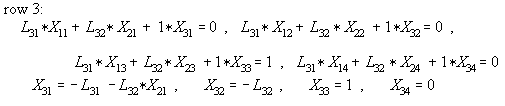
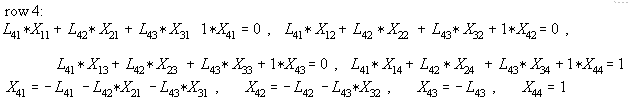
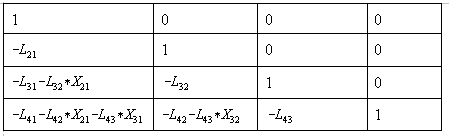 Eq. (8)
Eq. (8)
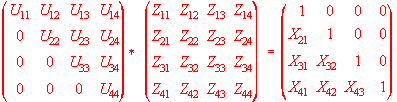 Eq. (9)
Eq. (9)
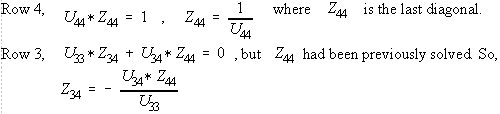
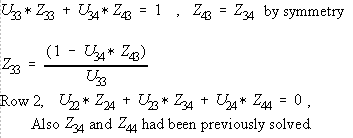
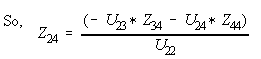
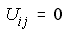 if no connection exists in Ybus, however
if no connection exists in Ybus, however
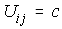 for a fill-in in LU after factoring Ybus, which is previously zero as no impedance is connected between i and j. Fill-ins are needed to solve the elements of Zbus. They become part of the LU.
for a fill-in in LU after factoring Ybus, which is previously zero as no impedance is connected between i and j. Fill-ins are needed to solve the elements of Zbus. They become part of the LU.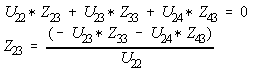
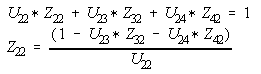

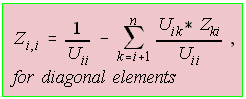 --- Eq. (10)
--- Eq. (10)















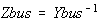 --- Eq.(1) and
--- Eq.(1) and
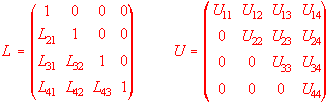 Eq. 6
Eq. 6
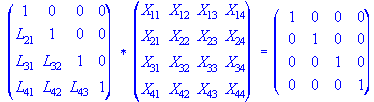 Eq. 7
Eq. 7
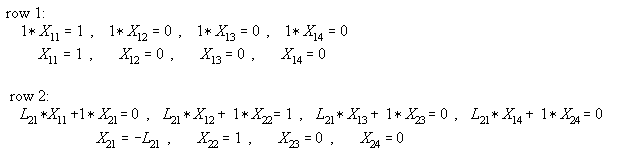
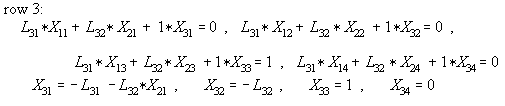
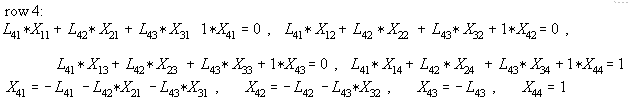
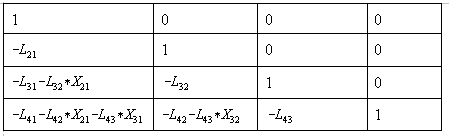 Eq. 8
Eq. 8
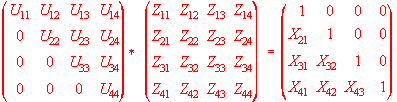 Eq. 9
Eq. 9
 Eq. 10
Eq. 10
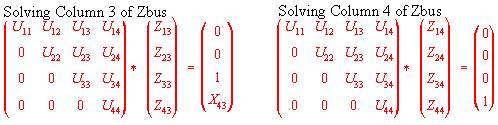
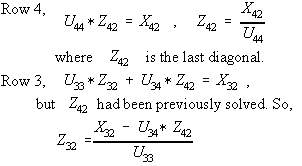
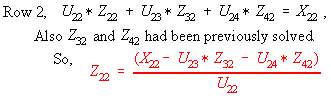 Eq. 11
Eq. 11
 Eq. 12
Eq. 12


